역방향전파(Backpropagation) | 패스트캠퍼스 챌린지 07일차

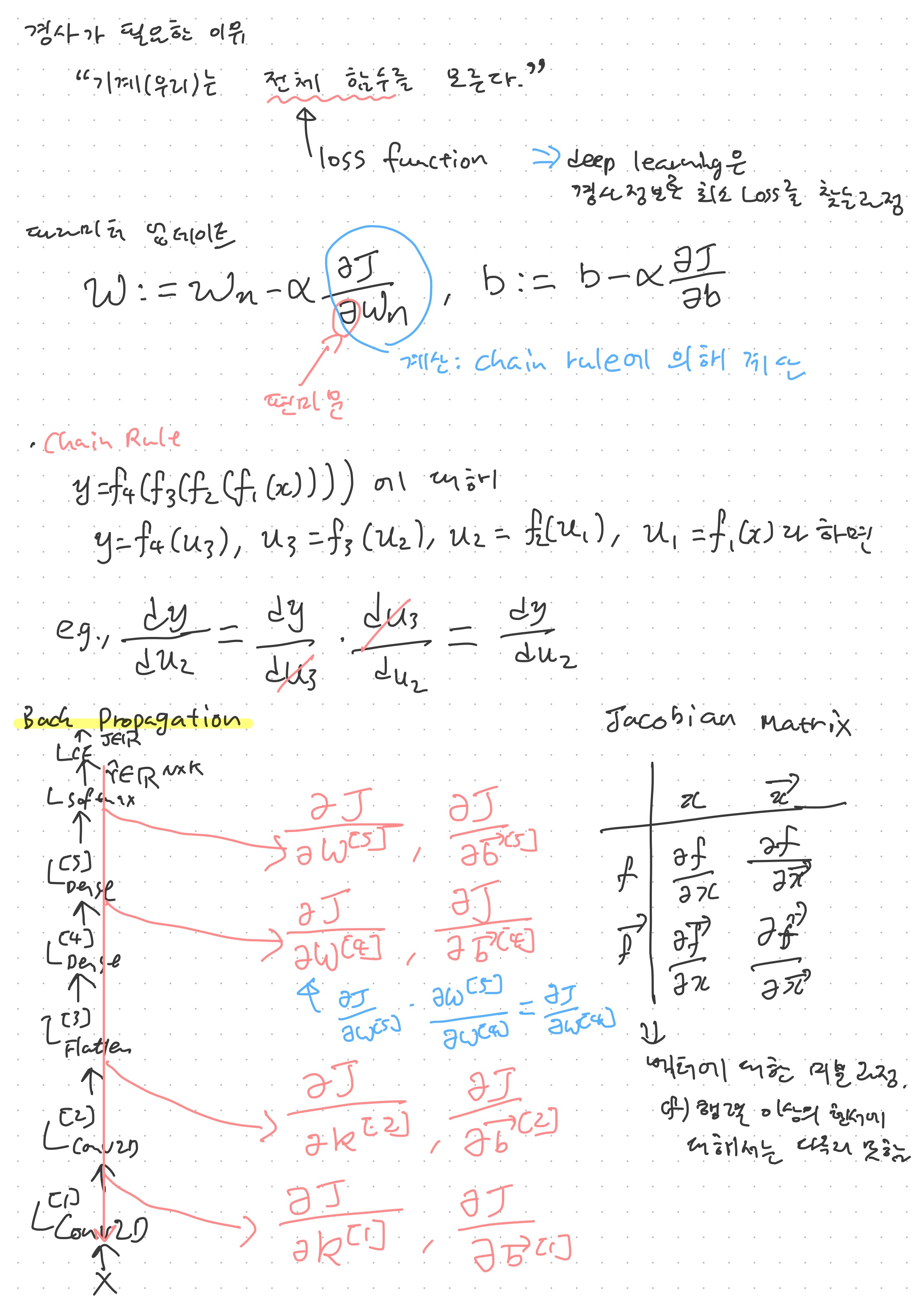
지금까지 순방향전파를 통해 데이터로부터 자질을 추출하고, 이를 분류하는 과정을 거쳤다면 역방향전파(backproragation)을 통해 실질적으로 학습을 진행할 때이다. 인공뉴런은 가중치(Weight)와 편항(Bias)이라는 파라미터를 가진 parameteric function이라는 내용을 다루었었다. 이러한 파라미터가 바로 학습의 대상이다. 학습에는 편미분이 사용되는데, x라는 변수에 대한 함수의 기울기를 구하는 일반적인 미분과 달리 편미분은 변수가 여러개일 때 그 중 한 변수에 대해서 기울기를 정하는 것인데, 강의에서 다음에 자세히 다루긴 하겠지만 공통적으로 chain rule이 적용되는 등 특징은 비슷한 듯 하다.
앞서 미분은 기울기라고 이야기 했는데, 구체적으로 미분은 함수의 결괏값 y를 최소한으로 만드는 과정이라고 볼 수 있다. 즉, 미분계수 dy/dx가 0보다 크다면 왼쪽으로 이동하는 것이고, 0보다 작으면 오른쪽으로 이동하는 것이며, 이동의 정도는 dy/dx의 절댓값에 비례한다. 이는 많은 책에서 이야기하듯 미분계수만큼의 기울기를 가지는 그래프를 그린 뒤, 해당 그래프에 공을 떨어뜨리는 것을 상상해 보면 된다.
구체적으로 x 를 x-dy/dx로 업데이트 해서 최소한의 y값을 가지는 x값을 찾아나설 수 있다. 다만, 이 때 미분계수를 그대로 사용하게 되면 변화의 폭이 너무 커서 결국은 수평위치에서 왔다갔다 해 버리는 결과를 초래할 수 있다. 이를 보완하기 위해 학습률(learning rate)라는 개념이 도입되게 된다. 학습률은 대게 1보다 작은 수치로, 가령 미분계수가 4일 때 x를 4만큼 움직이는 대신 0.1의 학습률을 적용해 0.4만큼만 움직여서 느리지만 최솟값으로 진행될 수 있도록 하는 역할을 한다.
이런 과정을 거쳐서 최솟값을 찾는 이유는 노트의 y=x^2의 그래프와 달리 실전에서는 이러한 함수의 정확한 모양을 알 수 없기 때문이다. 딥러닝에서 이 함수는 실질적으로 Loss Function인데, 이 Loss Function의 모양이 실제로 어떠한지는 데이터마다 다르기 때문에 알 수가 없다. 하지만 미분계수를 일반화 한 도함수를 안다면 미분계수를 구할 수는 있다. 이러한 성질을 이용하여 경사 정보를 활용해 loss가 최소가 되는 값을 찾는것이다.
이 때 실질적으로 미분계수를 구하기 위해 적용되는 중요한 규칙이 chain rule이다. 결과적으로 보자면 chain rule은 (편)미분 계수 사이의 일종의 분수 계산을 가능하게 한다. 즉, 미분계수 표기는 분수의 모양을 빌려 온 것이지 실질적으로 분수 계산은 아니다. 그렇지만 결과적으로는 마치 분수과 같이 dy/dx * dx/dz = dy/dz라는 계산이 성립하게 되는데, 이는 편미분에서도 마찬가지인 듯 하게 적용되었다. 이러한 원리를 이용하여, 각 레이어의 결괏값과 편향, 그리고 가중치의 미분값을 계산할 수 있다.
여기서 문제는 딥러닝에서는 입력값부터 결괏값, 가중치, 그리고 편향이 스칼라인 경우가 거의 없다는 것이다. 벡터, 행렬을 넘어서 다차원 텐서에 해당하는 값을 주로 다루는데, 스칼라가 아닌 텐서에서도 미분이나 편미분 계산이 그대로 이루어지는 검증해 보아야 한다. 적어도 벡터에 대해서는 Jacobian matrix를 통해 계산이 가능하다.
본격적으로 역방향전파 이야기가 나왔다. 편미분이라는 수학적 과정이 적극적으로 활용될 때이다. 아직까지는 따라잡을 만 한데, 본격적인 편미분 계산이 들어가면 인문사회계 출신으로 얼마나 따라잡을 수 있을지가 걱정이 되기도 한다. 하지만 제대로 이렇게 수학적인 개념을 잡고 넘어가는 것이 앞으로 Loss function을 설계하는 데에도 중요한 역할을 할 것이라 생각된다. 열심히 해야지.
본 포스팅은 패스트캠퍼스 환급 챌린지 참여를 위해 작성되었습니다. https://bit.ly/37BpXi