편미분과 인공뉴런 | 손실함수의 편미분 | 패스트캠퍼스 챌린지 10일차

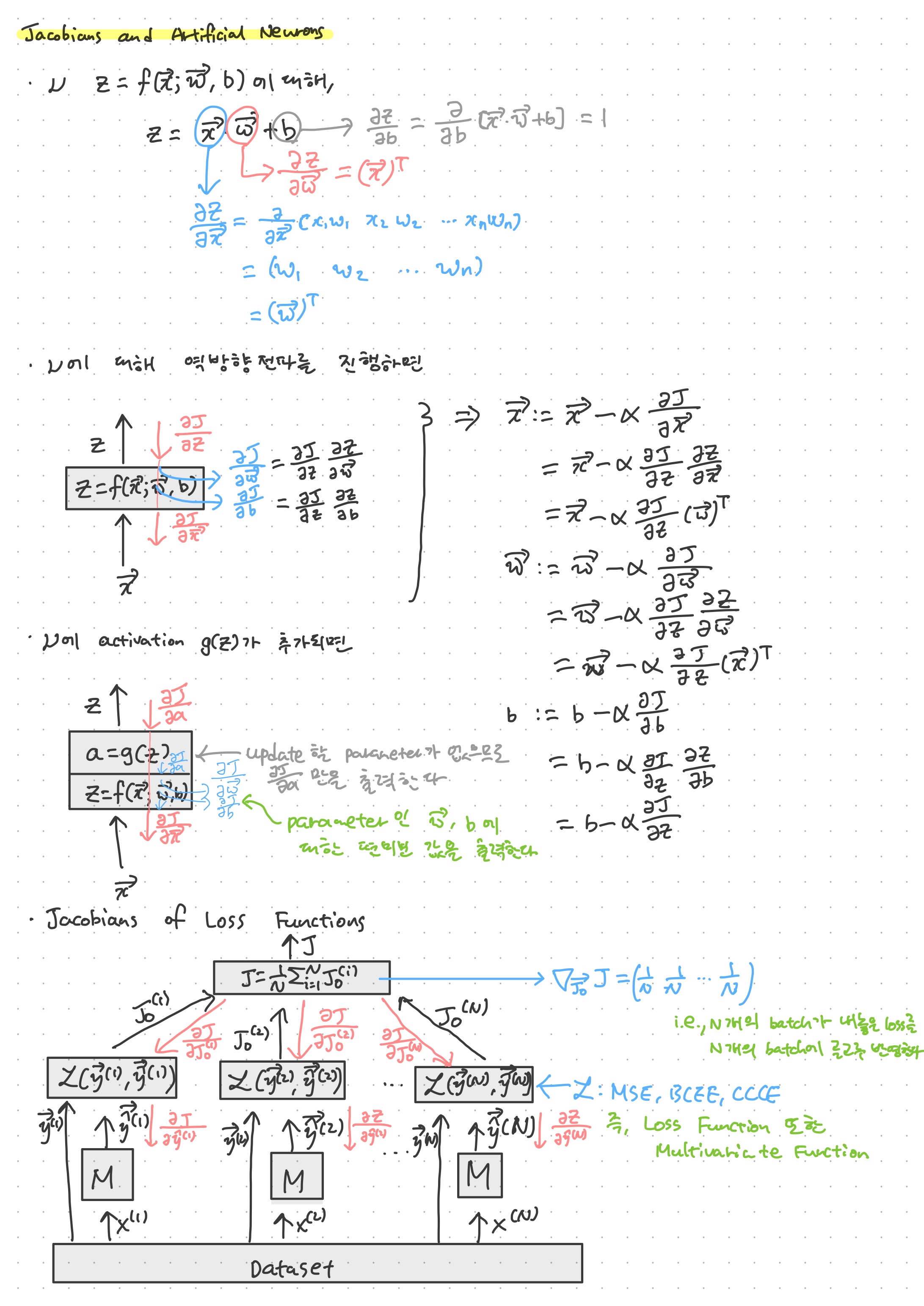
다변수함수와 편미분을 다룬 이유는 결국 인공 뉴런 또한 입력 벡터와 가중치 벡터, 그리고 편향 스칼라라는 세 개의 변수를 가지는 다변수함수이기 때문이다. 즉, 이 다변수함수를 거치면 입력 \vec{x}에 대한 편미분 뿐만 아니라 가중치 벡터 \vec{w}에 대한 편미분, 그리고 편향 b에 대한 편미분값(경사Gradient = Jacobian)을 가질 수 있다. 이 때, \vec{x}에 대한 편미분은 \vec{w}의 전치행렬, \vec{w}에 대한 편미분은 \vec{x}의 전치행렬이며, b에 대한 편미분은 1이다. 따라서, 하나의 인공 뉴런을 역방향전파할때면 손실값 J에 대해 ∂J/∂z를 입력으로 받아, chain rule에 의해 입력 벡터와 가중치 벡터, 그리고 편향 스칼라를 업데이트하게 되는데, 이 때 손실값을 줄일 수 있도록 업데이트시킨다.

활성화함수가 인공뉴런에 접목되었어도 크게 달라지는 건 없다. 이는 활성화함수에는 파라미터가 없기 때문이다. 즉, 활성화함수는 입력 변수를 하나만 받는 함수이기 때문에 그냥 미분을 하면 그만이고, 이 미분값이 affine function에 들어가 파라미터 업데이트를 진행하게 된다. 

손실함수의 경사를 생각할때에는 미니배치 문제를 생각해야 한다. 첫 번째 필기의 하단 그림과 같이 N개의 미니배치가 동일한 모델 M에 들어간다고 할 때, 각 모델의 결과는 각 손실함수를 가지며, 이 결과는 평균이 취해지게 되어 최종 손실값이 계산이 된다. 이러한 평균 함수를 경사로 역방향전파하면 1/N이 N개 있는 행벡터가 나오게 된다. 이는 N개의 미니배치가 내 놓은 결과를 공평하게 평균을 내어 반영하고, 그 결과 또한 공평하게 분배하여 학습을 진행할 수 있도록 한다는 의미가 된다. 실제로 모델에 전달되는 mean squared error, cross entropy error 등의 y_hat에 대한 편미분값은 chain rule에 의해 해당 함수의 편미분 함수에 1/N을 곱한 모양이 된다. MSE와 BCEE, CCEE의 y_hat에 대한 편미분 공식은 차근차근이 계산해 보면 도달할 수 있다. 그저 '변수 x_i에 대해 편미분을 계산할 떄는 나머지 입력 변수들을 상수취급한다'라는 원칙만 지킨 채 계산하면 크게 어렵지 않다. 손실함수라고 하기는 힘들지만 softmax 레이어 또한 마찬가지로 생각해 볼 수 있따.

---

편미분 과정을 통해 경사하강법을 진행해 학습을 이룬다라는 사실은 딥러닝을 공부할 떄 너무나도 당연하게 나와서 넘어갔지만, 생각해보면 그 메커니즘을 생각도 못 해 봤다. 무엇보다도 편미분이라는 새로운 개념이 너무 두렵게 느껴졌기 때문이다. 학위논문을 쓸때도 RNN이 편미분과정 때문에 경사소실 문제가 발생한다는 내용을 쓰기는 했지만, 정작 어떻게 경사소실이 이루어지는지는 이해하지 못했다. 지금이라도 이렇게 편미분이 사실은 크게 어렵지 않다는 사실을 익히고, 공식 하나하나를 편미분 해 가면서 식을 유도해 보는 기회를 가질 수 있어서 다행이다.

---

본 포스팅은 패스트캠퍼스 환급 챌린지 참여를 위해 작성되었습니다. https://bit.ly/37BpXi